巴黎地铁

刚才在看泛函分析的视频的时候看到一个好玩的问题，设 \(E\) 是巴黎所有地铁站的集合，\(d:E\times E\to\mathbb{R}\) 定义为 \(d(x,y)\) 为 \(x\) 站到达 \(y\) 站的平均最快时间，问这个函数是不是一个距离函数。

根据“时间”的定义显然 \(d(x,y)\geq 0\) 而且 \(d(x,y)=0\implies x=y\)。由于是“最快时间”，所以三角不等式 \(d(x,y)\leq d(x,z)+d(z,y)\) 也成立。最后剩下对称条件 \(d(x,y)=d(y,x)\)。乍看应该成立，从 Gare du Nord 到 Rome 的平均最快时间的确等于 Rome 去 Gare du Nord 的平均最快时间，但下面这张图给了个反例。

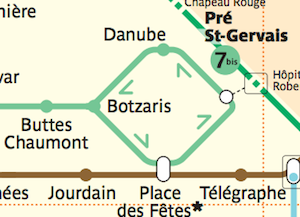
由于巴黎地铁某些地方存在单向性…所以从 Botzaris 和 Danube 之间的时间不一样-__-