FEniCS
既然之前保证过的,那么就现在有点时间介绍下我现在用的有限元计算软件 FEniCS。由于设计数值计算,所以把这篇博文归类到数学里面去了。
首先要注意,我说的是广义上的有限元计算,并不仅限于我的本行力学。这个软件所做的,就是用有限元方法数值求解一个偏微分方程(组)。也就是说,你需要做的,就是得告诉程序
- 你要求解的方程是什么。要注意,必须采用 Formulation faible/variationnelle 而不能采用强形式。这个大家做有限元的都知道。
- 定义几何,更具体的说就是定义一个 Maillage。
- 你想用什么有限元求解方程,也就是说定义 Espace de discrétisation。
至于其他琐碎的事情比如 Assemblage 之类的 FEniCS 会自动帮你做,这就是它强大的地方。此外你可操控的自由度也很大,你可以自己选择 Schéma d’intégration,选择线性方程组的求解方法之类的。
下面简单举个例子,就拿最最常见的 Poisson 下手吧。
\[-\Delta u=f\text{ on }\Omega=[0,1]^2\]其中我们假设外力 \(f\) 等于
\[f(x,y)=\sin(\pi x)\sin(\pi y)\]此外边界条件为最简单的 \(u=0\) 在 \(\partial\Omega\) 上。
第一步就是把强形式变成弱形式了,得到寻找 \(u\in H^1_0(\Omega)\),使得对于所有 \(v\in H^1_0(\Omega)\),有
\[a(u,v)=\int_\Omega\nabla u\cdot \nabla v\,\mathrm{d}x=\int_\Omega f\,v\,\mathrm{d}x=L(v)\]然后就可以打开你们喜欢的编辑器开始 Python 啦!第一步从加载 FEniCS 包开始
from dolfin import *
然后我们定义几何空间并网格化,FEniCS 里面有一个函数可以定义二维单位平方,所以我们直接使用就好了。在一般情况下你可能需要自己在 FEniCS 里面定义几何然后用 CGAL 去 Mailler,或者一开始从几何开始就用其他的 Mailleur,比如 GMSH。
n = 100
mesh = UnitSquareMesh(n, n)
这里我们把 \(\Omega=[0,1]^2\) 用三角形单元进行划分,每边有100个三角形的边。如果需要 Raffiner 那么只需要变大 \(n\) 就好了。
然后我们定义有限元函数空间。还记得当初在巴黎 CDD 的时候来过一个小教授讲了有限差分法和有限元法的区别,他讲得很好,就是说 DF 去近似的是导数,把各种导数用有限差分去代替;而有限元则是直接去近似函数,即把无线维函数空间用一个有限维函数空间去代替。
V = FunctionSpace(mesh, 'CG', 1)
u, v = TrialFunction(V), TestFunction(V)
U = Function(V)
这里 V 就是我们的有限元空间,CG 代表我们采用最普遍的 Lagrange 有限元,阶数是1,即每个三角形单元上我们用线性函数去近似解。其次的 u 和 v 定义了弱形式中的解和测试函数,而 U 定义了一个 \(V\) 上的函数,之后用来放置解。
现在开始定义外力 \(f\),在 FEniCS 中很简单,只需要做
f = Expression('sin(pi*x[0])*sin(pi*x[1])')
即可,在 Expression 中使用 C++ 语法定义一个函数,x[0] 代表第1个坐标 \(x\),x[1] 代表第2个坐标 \(y\)。
下面就要定义要求解的问题了,具体来说就要定义弱形式中的双线性形式 \(a\) 和线性形式 \(L\)
a = inner(grad(u), grad(v))*dx
L = f*v*dx
是不是很简单,连解释都免了。之后就差定义边界条件了,我们有
def bord(x, on_boundary):
return on_boundary
bc = DirichletBC(V, Constant(0.0), bord)
其中 bord 定义了边界,on_boundary 是 FEniCS 提供的,意思就是在网格的边界上,由于我们这里的边界条件就是完全定义在边界上的,所以直接用就好了(否则需要自己定义一个在边界上对 x 的条件)。然后的 DirichletBC 函数定义一个 Dirichelet 的边界条件,也很直观吧。
最后就是求解了,我们有
solve(a == L, U, bc)
并把解存到我们之前定义的 U 中。之后如果想简单地看求解结果的话,只需要
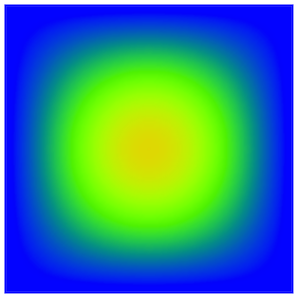
plot(U, interactive=True)
即可,是不是很简单!
留下评论